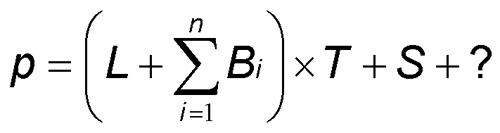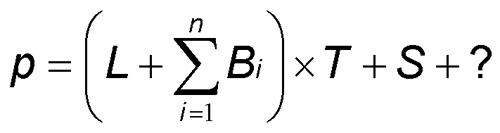
Let’s Write a Quake 3 Graphics Engine in OpenGL!
by Bryan McNett
Article 2
OpenGL commands for light-mapping, bump-mapping, texture-mapping and specular-mapping in Quake 3
Before you begin, you should read my article on Multitexture and the Quake 3 Graphics Engine. If you can, play with the accompanying Photoshop file to get a feel for texture editing in Quake 3. Now, let’s proceed to write a Quake 3 graphics engine in OpenGL!
This article will explain in plain language how to implement the multitexture effects of Quake 3 in the OpenGL graphics language. You are expected to understand a pseudocode that looks like C++. Concepts like the multiplication of colors should be familiar to you. Other Quake graphics technologies are not covered by this article. With the exception of dynamic LOD geometry management, you will find many fine tutorials on the remaining Quake graphics technologies in books and on the Internet. Please refer to them if you have any questions after reading this article.
It is possible to implement multitexture in OpenGL using its alpha blend unit, multiple texture units, or a combination of both. In May, 1998, very few people own multiple texture units. Correspondingly, Quake 3’s important multitexture effects should not require multiple texture units - but they will require an alpha blend unit. For this reason and for the sake of simplicity, this article will cover only the alpha blend unit.
First, I will explain what the alpha blend unit is and how it works.
Introducing OpenGL’s alpha blend unit
When OpenGL is drawing a polygon, it has the option of blending the polygon with the colors already on the screen. This is customarily called "alpha blending".
The following OpenGL function controls the blending process:
void
BlendFunc ( enum src, enum dst ) ;For example, the following OpenGL function makes all subsequent polygons translucent:
BlendFunc
( SRC_ALPHA, ONE_MINUS_SRC_ALPHA ) ;…and the following OpenGL function makes all subsequent polygons opaque:
BlendFunc
( ONE, ZERO ) ;Unless you understand the inner workings of the alpha blend unit, however, it may not be clear what the terms SRC_ALPHA, ONE_MINUS_SRC_ALPHA, ONE, or ZERO are supposed to mean in this context. Now to explain:
How does the alpha blend unit work?
Once this OpenGL function is called:
void
BlendFunc ( enum src, enum dst ) ;The alpha blend unit blends subsequent polygons with the screen via the following function, which is executed once for each pixel in each polygon:
screen = polygon * src + screen * dst;
How does the alpha blend unit make translucent polygons?
When we plug the following terms into the function:
BlendFunc
( SRC_ALPHA, ONE_MINUS_SRC_ALPHA ) ;We can replace
src and dest in the above pseudocode with alpha and 1-alpha:screen = polygon * alpha + screen * (1-alpha);
alpha
represents the opacity of the polygon. alpha can be a constant value, it can come from a texture map, or it can come from "Gouraud shading".
We can simplify the above pseudocode when
alpha is equal to one:screen = polygon * 1 + screen * 0;
or simplified further…
screen = polygon;
And where
alpha is equal to zero, we can simplify the pseudocode so:screen = polygon * 0 + screen * 1;
or simplified further…
screen = screen;
Therefore, as
alpha varies from zero to one, the polygon varies from complete transparency to complete opacity. This is a translucent polygon, as we have noted before.
How does the alpha blend unit make opaque polygons?
When we plug these terms into OpenGL’s alpha blending function:
BlendFunc
( ONE, ZERO ) ;The pseudocode executes as follows:
screen = polygon * 1 + screen * 0;
Algebra can simplify this to the following:
screen = polygon;
Therefore, no blending takes place. The polygon is copied directly to the screen. This is an opaque polygon, as we have noted before.
Adding and multiplying polygons using the alpha blend unit
Just as it is possible to draw an opaque or a translucent polygon, it is possible to add a polygon to the screen, or to multiply the screen by a polygon. If this makes no sense to you, you may wish to refer to Multitexture and the Quake 3 Graphics Engine, which attempts to explain these ideas using plain language.
Adding a polygon to the screen
To add subsequent polygons to the screen, issue the following OpenGL command:
BlendFunc
( ONE, ONE ) ;The pseudocode is as follows:
screen = polygon * 1 + screen * 1;
which can be simplified via algebra to the following:
screen = polygon + screen;
Clearly, subsequent polygons will be added to the screen, as we noted previously.
Multiplying the screen by a polygon
To multiply the screen by subsequent polygons, issue the following OpenGL command:
BlendFunc
( DST_COLOR, ZERO ) ;The pseudocode is as follows:
screen = polygon * screen + screen * 0;
which can be simplified to the following:
screen = polygon * screen;
Clearly, the screen will be multiplied by subsequent polygons, as we noted previously.
Surprise! You now know the three OpenGL functions for multitexture in Quake 3!
You may not realize that we’ve just covered the three OpenGL commands used for multitexture in Quake 3:
BlendFunc(ONE,ZERO); // copy the polygon to the screen BlendFunc(ONE,ONE); // add the polygon to the screen BlendFunc(DST_COLOR,ZERO); // multiply the polygon with the screen
The following code fragment tells you where these three commands are used:
// we now begin drawing one polygon BlendFunc( ONE, ZERO ) ; // screen = polygon // draw the light map here BlendFunc ( ONE, ONE ) ; // screen = screen + polygon // draw all the bump maps here BlendFunc ( DST_COLOR, ZERO ) ; // screen = screen * polygon // draw the texture map here BlendFunc ( ONE, ONE ) ; // screen = screen + polygon // draw the specular map here // we now end drawing one polygon
note: To copy polygons without blending in the real world, you will probably want to disable alpha blending with Disable(BLEND) rather than by calling BlendFunc(ONE,ZERO)! We use BlendFunc(ONE,ZERO) only as an example to help explain the concept of blending.
Let’s extract the pseudocode from the comments on the right:
screen = polygon screen = screen + polygon screen = screen * polygon screen = screen + polygon
Now let’s replace the word "polygon" with the names of the respective maps:
screen = light screen = screen + bumps screen = screen * texture screen = screen + specular
using algebra, we can simplify further…
screen = (light + bumps) * texture + specular
Hey… this looks a lot like the equation from Multitexture and the Quake 3 Graphics Engine: